数据结构与算法（八）——排序算法

数据结构与算法

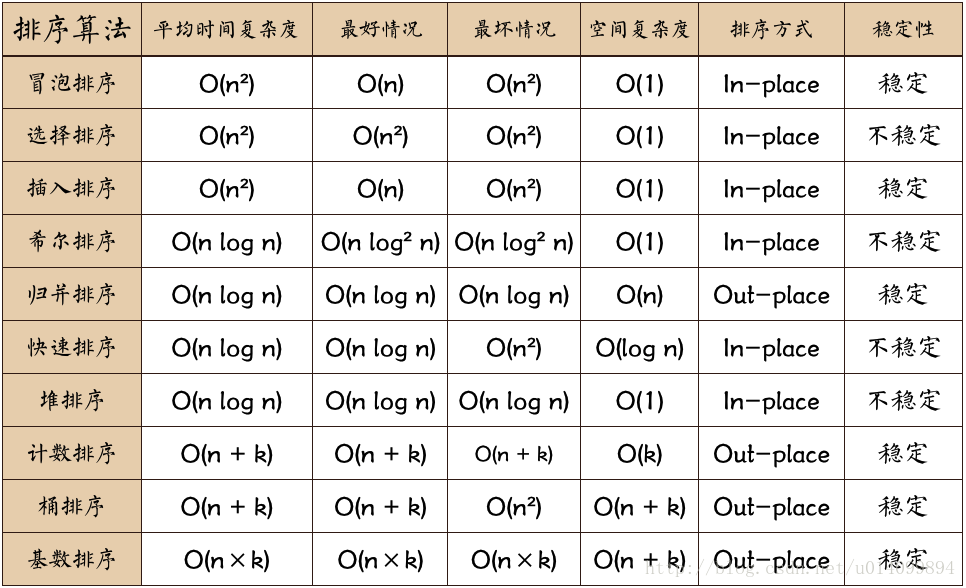
常见的排序算法总结

数据结构与算法（八）——排序算法_2020-02-20-16-44-05.png

排序的稳定性

因为待排序的记录序列中可能存在两个或两个以上的关键字相等的记录， 排序结果可能会存在不唯一的情况。所以就有稳定与不稳定的定义。

假设 ki=kj( 1 =< i <= n,1 =< j <= n, i != j)，且在排序前的序列中 ri 领先于 rj。如果排序后 ri 仍领先于 rj，则称所用的排序方法是稳定的；反之，若可能使得排序后的序列中 rj 领先于 ri，则称所用的排序方法是不稳定的。只要有一组关键字发生类似情况，就可认为此排序方法是不稳定的。

内排序和外排序

根据在排序过程中待排序记录是否全部放在内存中，排序分为内排序和外排序。

  • 内排序是在排序整个过程中，待排序的所有记录全部被放置在内存中。
  • 外排序是由于排序的记录个数太多，不能同时放置在内存中，整个排序过程需要在内外存之间多次交换数据才能进行。

内排序，排序算法的性能主要有 3 个影响因素：

  • 时间性能
    排序算法的时间开销是衡量其好坏的最重要的标志。
    在内排序中，主要进行两种操作：比较和移动。
    高效率的内排序算法应该具有尽可能少的关键字比较次数和尽可能少的记录移动次数。
  • 辅助空间
    评估算法的另一个主要标准是执行算法所需要的辅助存储空间。
    辅助存储空间是除了存放待排序所占用的存储空间外，执行算法所需要的其他存储空间。
  • 算法的复杂性
    指算法本身的复杂性，过于复杂的算法也会影响排序的性能。

冒泡排序

基本思想

两两比较相邻记录的关键字，如果反序则交换，直到没有反序的记录为止。

算法复杂度分析

  • 最好：仅需要 n - 1 次比较，时间复杂度为 O(n)；
  • 最坏：需要 n(n - 1)/2 次比较和交换；
  • 平均：复杂度为 O(n2)。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class BubbleSort {

   // 最简单交换排序，非冒泡排序,比较的不是相邻关键字，但便于理解
   // 比较次数n(n + 1)/2，交换次数会很多，仔细分析下，会把小的数字放到最后去，而冒泡则不会，原因就是比较的是相邻关键字
   static void simpleSwapSort(int[] array) {
       if (array == null || array.length == 0 || array.length == 1) return;

       for (int i = 0, size = array.length; i < size; ++i) {
           //for (int j = 0; j < size; j++) { //这种效率更低 n^2
           for (int j = i + 1; j < size; ++j) {
               if (array[j] < array[i]) {
                   CommonUtil.swap(array, i, j);
               }
           }
       }
   }

   // 正宗的冒泡排序，从最底下开始冒泡，两两比较,每次都将小的往上冒一点
   static void bubbleSort(int[] array) {
       if (array == null || array.length == 0 || array.length == 1) return;

       for (int i = 1, size = array.length; i < size; ++i) {
           for (int j = size - 1; j >= i; --j) {
               if (array[j] < array[j - 1]) {
                   CommonUtil.swap(array, j, j - 1);
               }
           }
           //CommonUtil.printArray(array);
       }
   }

   // 冒泡排序优化，如果经过一轮发现已经是有序的，就不再进行排序
   static void bubbleSortBetter(int[] array) {
       if (array == null || array.length == 0 || array.length == 1) return;

       boolean flag = true;
       for (int i = 1, size = array.length; i < size && flag; ++i) {
           flag = false;
           for (int j = size - 1; j >= i; --j) {//经过一轮循环，发现两两已经是有序的了，就置为false
               if (array[j] < array[j - 1]) {
                   CommonUtil.swap(array, j, j - 1);
                   flag = true;
               }
           }
           //CommonUtil.printArray(array);
       }
   }
}

直接插入排序

基本思想

将一个记录插入到已经排好序的有序表中，从而得到一个新的、记录递增 1 的有序表。插入排序是进行值移动，而非值交换。所以在量较小的情况下插入排序性能要优于冒泡和简单选择排序。

算法复杂度分析

  • 最好，只需进行比较 n - 1 次，无需进行移动；
  • 最坏的情况下，比较(n + 2)(n - 1)/2 次，交换(n + 4)(n - 1)/2 次。
  • 平均：复杂度 O(n2)

java 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class StraightInsertionSort {
    //for循环
    static void straightInsertionSort2(int[] array) {
        if (array == null || array.length == 0 || array.length == 1) return;

        for (int i = 1, j, temp, size = array.length; i < size; ++i) {
            temp = array[i];
            for (j = i - 1; j >= 0 && array[j] > temp; --j) {
                array[j + 1] = array[j];//移动而非交换
            }
            array[j + 1] = temp;
        }
    }
}

简单选择排序

基本思想

每一次遍历时选取关键字最小的记录作为有序序列的第 i 个记录。

算法复杂度分析

  • 最好最差的情况，都要进行 n(n-1)/2 次比较；在最好的情况下，不需要进行交换，在最坏的情况下，进行 n-1 次交换。
  • 平均：复杂度为 O(n2)。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class SimpleSelectionSort {
    static void simpleSelectionSort(int[] array) {
        if (array == null || array.length == 0 || array.length == 1) return;

        for (int i = 0, size = array.length; i < size; ++i) {
            int minIndex = i;

            for (int j = i + 1; j < size; ++j) {
                if (array[j] < array[minIndex]) {
                    minIndex = j;
                }
            }

            if (minIndex != i) {
                CommonUtil.swap(array, i, minIndex);
            }
        }
    }
}

冒泡排序和插入排序的时间复杂度都是 O(n2)，都是原地排序算法，为什么插入排序要比冒泡排序更受欢迎呢？

冒泡排序的数据交换要比插入排序的数据移动要复杂，冒泡排序需要 3 个赋值操作，而插入排序只需要 1 个。

归并排序

基本思想

归并排序的核心思想还是蛮简单的。如果要排序一个数组，我们先把数组从中间分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了。

归并排序使用的就是分治思想。分治，顾名思义，就是分而治之，将一个大问题分解成小的子问题来解决。小的子问题解决了，大问题也就解决了。分治算法一般都是用递归来实现的。

算法复杂度分析

归并排序的时间复杂度为 O(nlogn)

java实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102


public static void main(String[] args) {
    int[] arrays = {9, 2, 5, 1, 3, 2, 9, 5, 2, 1, 8};
    mergeSort(arrays, 0, arrays.length - 1);

    System.out.println("公众号：Java3y" + arrays);


}

/**
 * 归并排序
 *
 * @param arrays
 * @param L      指向数组第一个元素
 * @param R      指向数组最后一个元素
 */
public static void mergeSort(int[] arrays, int L, int R) {

    //如果只有一个元素，那就不用排序了
    if (L == R) {
        return;
    } else {

        //取中间的数，进行拆分
        int M = (L + R) / 2;

        //左边的数不断进行拆分
        mergeSort(arrays, L, M);

        //右边的数不断进行拆分
        mergeSort(arrays, M + 1, R);

        //合并
        merge(arrays, L, M + 1, R);

    }
}


/**
 * 合并数组
 *
 * @param arrays
 * @param L      指向数组第一个元素
 * @param M      指向数组分隔的元素
 * @param R      指向数组最后的元素
 */
public static void merge(int[] arrays, int L, int M, int R) {

    //左边的数组的大小
    int[] leftArray = new int[M - L];

    //右边的数组大小
    int[] rightArray = new int[R - M + 1];

    //往这两个数组填充数据
    for (int i = L; i < M; i++) {
        leftArray[i - L] = arrays[i];
    }
    for (int i = M; i <= R; i++) {
        rightArray[i - M] = arrays[i];
    }


    int i = 0, j = 0;
    // arrays数组的第一个元素
    int  k = L;


    //比较这两个数组的值，哪个小，就往数组上放
    while (i < leftArray.length && j < rightArray.length) {

        //谁比较小，谁将元素放入大数组中,移动指针，继续比较下一个
        if (leftArray[i] < rightArray[j]) {
            arrays[k] = leftArray[i];

            i++;
            k++;
        } else {
            arrays[k] = rightArray[j];
            j++;
            k++;
        }
    }

    //如果左边的数组还没比较完，右边的数都已经完了，那么将左边的数抄到大数组中(剩下的都是大数字)
    while (i < leftArray.length) {
        arrays[k] = leftArray[i];

        i++;
        k++;
    }
    //如果右边的数组还没比较完，左边的数都已经完了，那么将右边的数抄到大数组中(剩下的都是大数字)
    while (j < rightArray.length) {
        arrays[k] = rightArray[j];

        k++;
        j++;
    }
}

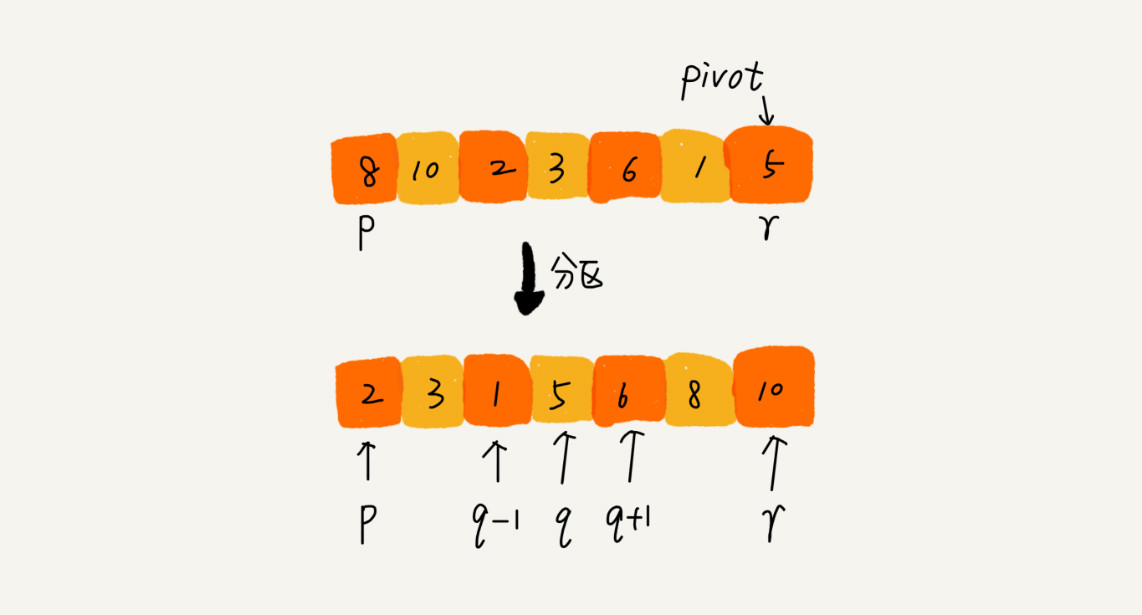
快速排序

基本思想

如果要排序数组中下标从 p 到 r 之间的一组数据，我们选择 p 到 r 之间的任意一个数据作为 pivot（分区点）。

我们遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放到中间。经过这一步骤之后，数组 p 到 r 之间的数据就被分成了三个部分，前面 p 到 q-1 之间都是小于 pivot 的，中间是 pivot，后面的 q+1 到 r 之间是大于 pivot 的。

根据分治、递归的处理思想，我们可以用递归排序下标从 p 到 q-1 之间的数据和下标从 q+1 到 r 之间的数据，直到区间缩小为 1，就说明所有的数据都有序了。

数据结构与算法（八）——排序算法_2021-04-01-13-48-03.png

算法复杂度分析

  • 最坏：待排序为正序或逆序，这样每次分割后的子序列一个之比上一次序列少一个元素，一个为空。如 1 2 3 4 5 pivotkey=1;分割后一个序列为 2 3 4 5 一个为空，最终 O(n^2)
  • 最好：每一次分割都能平分，很均匀 O(nlogn)
  • 平均：O(n*logn) 数学归纳法

java 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
class QuickSortWhile {
    private static final int MAX_LIMIT = 4;

    static void quickSort(int[] arr) {
        if (array == null || array.length == 0 || array.length == 1) return;

        quick_sort_recursive(arr, 0, arr.length - 1);
    }

    private static void quick_sort_recursive(int[] arr, int start, int end) {
        if (end - start <= MAX_LIMIT) {
            // 到达一定程度的小数组时使用插入排序
            insertSort(arr, start, end);
            return;
        }

        while (start < end) { //尾递归优化
            int pivot = partition(arr, start, end);

            quick_sort_recursive(arr, start, pivot - 1);

            start = pivot + 1;
        }
    }

    /*
       分区操作：将arr[end]作为中轴，比它小的放在前面，比它大的放在后面
    */
    private static int partition(int[] arr, int start, int end) {
        int pivotKey = arr[end];

        int left = start, right = end - 1;

        while (left < right) {

            while (arr[left] <= pivotKey && left < right) left++;
            while (arr[right] >= pivotKey && left < right) right--;

            if (left < right) {
                CommonUtil.swap(arr, left, right);
            }
        }

        if (arr[left] >= pivotKey) {
            CommonUtil.swap(arr, left, end);
        } else {
            left++;
        }

        return left;
    }

    //插入排序
    private static void insertSort(int[] arr, int start, int end) {

        for (int i = start + 1, j, temp; i <= end; ++i) {
            temp = arr[i];
            j = i - 1;

            while (j >= start && arr[j] > temp) {
                arr[j + 1] = arr[j];
                j--;
            }

            arr[j + 1] = temp;
        }

    }
}

二分插入排序

基本思想

二分（折半）插入排序是一种在直接插入排序算法上进行小改动的排序算法。其与直接排序算法最大的区别在于查找插入位置时使用的是二分查找的方式，在速度上有一定提升。

算法复杂度分析

插入每个记录需要 O(log i)比较，最多移动 i+1 次，最少 2 次。

  • 最佳： O(n log n)，
  • 最差：O(n^2)
  • 平均: O(n^2)。

总排序码比较次数比直接插入排序的最差情况好得多，但比最好情况要差，所元素初始序列已经按排序码接近有序时，直接插入排序比二分插入排序比较次数少

java 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class BinaryInsertionSort {

    static void binaryInsertionSort(int[] array) {
        if (array == null || array.length == 0 || array.length == 1) return;

        int temp, left, right, middle;
        for (int i = 1, size = array.length; i < size; i++) {
            temp = array[i];
            left = 0;
            right = i - 1;

            //寻找合适的位置
            while (left <= right) {
                middle = (left + right) / 2;
                if (array[middle] > temp) {
                    right = middle - 1;
                } else {
                    left = middle + 1;
                }
            }

            for (int j = i - 1; j >= left; j--) {
                array[j + 1] = array[j];
            }

            array[left] = temp;
        }

    }
}

希尔排序

也称递减增量排序算法，是插入排序的一种更高效的改进版本。希尔排序是非稳定排序算法。

希尔排序是基于插入排序的以下两点性质而提出改进方法的：

  • 插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率
  • 但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位

基本思想

希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能。这样可以让一个元素可以一次性地朝最终位置前进一大步。然后算法再取越来越小的步长进行排序，算法的最后一步就是普通的插入排序，但是到了这步，需排序的数据几乎是已排好的了（此时插入排序较快）。

假设有一个很小的数据在一个已按升序排好序的数组的末端。如果用复杂度为 O(n2)的排序（冒泡排序或插入排序），可能会进行 n 次的比较和交换才能将该数据移至正确位置。而希尔排序会用较大的步长移动数据，所以小数据只需进行少数比较和交换即可到正确位置。

一个更好理解的希尔排序实现：将数组列在一个表中并对列排序（用插入排序）。重复这过程，不过每次用更长的列来进行。最后整个表就只有一列了。将数组转换至表是为了更好地理解这算法，算法本身仅仅对原数组进行排序（通过增加索引的步长，例如是用 i += step_size 而不是 i++ ）。

例如，假设有这样一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ]，如果我们以步长为 5 开始进行排序，我们可以通过将这列表放在有 5 列的表中来更好地描述算法，这样他们就应该看起来是这样：

13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10

然后我们对每列进行排序：

10 14 73 25 23
13 27 94 33 39
25 59 94 65 82
45

将上述四行数字，依序接在一起时我们得到：[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ].这时 10 已经移至正确位置了，然后再以 3 为步长进行排序：

10 14 73
25 23 13
27 94 33
39 25 59
94 65 82
45

排序之后变为：

10 14 13
25 23 33
27 25 59
39 65 73
45 94 82
94

最后以 1 步长进行排序（此时就是简单的插入排序了）。

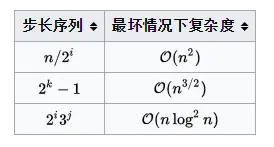
步长选择及复杂度

步长的选择是希尔排序的重要部分。只要最终步长为 1 任何步长序列都可以工作。
数据结构与算法（八）——排序算法_2020-02-23-23-05-25.png

  • 最优时间复杂度
    O(n)

  • 不稳定

java 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
package cc;

public class ShellSort {

    public static void shellsort(int[] a) {

        int n = a.length;

        int j;
        for(int d=n/2;d>0;d/=2) {/* 希尔增量序列 */
            /* 插入排序 */
            for(int p=d;p<n;p++) {
                int temp = a[p];
                for(j=p;j>=d && a[j-1] > temp;j=j-d)
                    a[j] = a[j-d];
                a[j] = temp;
            }
        }

    }
}

总结及参考资料

除了以上常见的排序算法，还有堆排序、桶排序、基数排序、计数排序等。
常见的排序算法

本文标题:数据结构与算法（八）——排序算法

文章作者:南有乔木

发布时间:2020-02-20, 16:41:54

最后更新:2021-04-01, 13:56:38

原始链接:http://yoursite.com/2020/02/20/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E4%B8%8E%E7%AE%97%E6%B3%95%EF%BC%88%E5%85%AB%EF%BC%89%E2%80%94%E2%80%94%E6%8E%92%E5%BA%8F%E7%AE%97%E6%B3%95/

许可协议: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。

文章目录
  1. 1. 常见的排序算法总结
  2. 2. 排序的稳定性
  3. 3. 内排序和外排序
  4. 4. 冒泡排序
    1. 4.1. 基本思想
    2. 4.2. 算法复杂度分析
    3. 4.3. 代码实现
  5. 5. 直接插入排序
    1. 5.1. 基本思想
    2. 5.2. 算法复杂度分析
    3. 5.3. java 实现
  6. 6. 简单选择排序
    1. 6.1. 基本思想
    2. 6.2. 算法复杂度分析
    3. 6.3. 代码实现
  7. 7. 冒泡排序和插入排序的时间复杂度都是 O(n2)，都是原地排序算法，为什么插入排序要比冒泡排序更受欢迎呢？
  8. 8. 归并排序
    1. 8.1. 基本思想
    2. 8.2. 算法复杂度分析
    3. 8.3. java实现
  9. 9. 快速排序
    1. 9.1. 基本思想
    2. 9.2. 算法复杂度分析
    3. 9.3. java 实现
  10. 10. 二分插入排序
    1. 10.1. 基本思想
    2. 10.2. 算法复杂度分析
    3. 10.3. java 实现
  11. 11. 希尔排序
    1. 11.1. 基本思想
    2. 11.2. 步长选择及复杂度
    3. 11.3. java 实现
  12. 12. 总结及参考资料
|